Geologica 1 - The Archdeacon of Calcutta and a Royal Astronomer in London suggested why mountains rise up high
The first episode of Geologica's journey to the discovery of the Earth: how the British topographic campaign in India led to the Isostasy Principle
With this article I would like to start a series that will take the reader on a journey to explore the dynamics of our planet. In the footsteps of the great scientists who with their discoveries and insights have advanced the knowledge of Geology we will see how, one step at a time, hypothesis after hypothesis, it was possible to build a unifying theory that explains the global functioning of our planet: the Theory of Plate Tectonics.
To begin, we will go to the mid-19th century. By that time, great geologists such as Scotsmen James Hutton and Charles Lyell (the latter a friend of Charles Darwin) had already laid the foundations of geology as an autonomous science, realizing that the phenomena that form the Earth required very long timescales and those of the past could be interpreted by observing the present.
One thing that was also known already was that the Earth’s surface shows very different elevations from the highest peak to the depth of the oceans. A statistical graph of the Earth’s elevations versus their percentage of the total highlights how major depths and peaks are the exception:
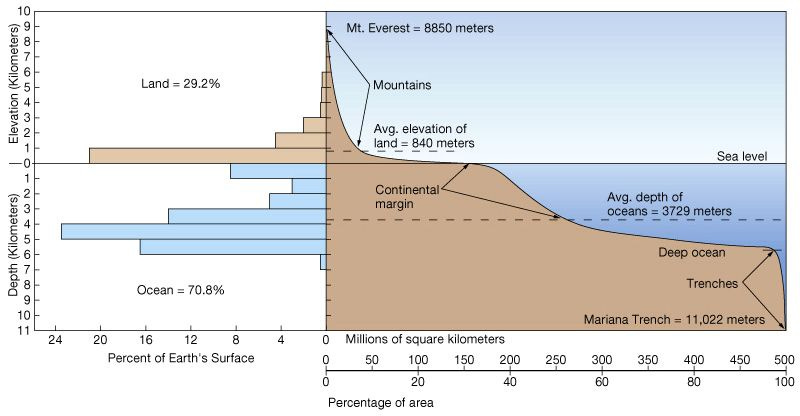
Why are there 2 major average elevations and 2 exceptions? Why do mountains rise up high and ocean trenches are so deep? Let’s start from the mountains.
Between 1840 and 1850, the Welsh geographer George Everest (1790 – 1866) led the Great Trigonometrical Survey survey of India. The survey, completed in 1971, led to great accomplishments such as the measurement of the height of the greatest Himalayan peaks like Mt. Everest and K2. For the first time, an accurate measurement of a section of an arc of longitude was also carried out.
In order to perform those measurements, beside new methods developed by Everest himself, also traditional methods were used: they were based on the traditional triangulation and on the position of a reference star at a certain time of the day. Both methods should give identical results, but in one case during the campaign it was not so: the measuring error of the distance between the two cities of Kaliana and Kalianpur, at 100 and 700 km from the Himalayan belt respectively, was too large. The triangulation method gave 150 km more than the astronomical one!
In 1854, Everest’s successor as head of the campaign Andrew Scott Waugh approached John Henry Pratt (1809-1871), a British mathematician, in an attempt to understand the issue. Pratt had been appointed Archbishop of Calcutta in 1850. He was born in London in 1809 and studied mathematics at Cambridge’s Caius College. While in India he was able to pursue his interest in mathematics and he was a renown expert of mathematical applications on gravitational physics.
Pratt showed Waugh how the error was to be found in the astronomical method: in order to determine the position of a star, the zenith direction (the vertical) must be exactly determined with a plumb line. Pratt suggested that the gravitational pull of both Himalaya and Tibetan plateau on the plumb line was stronger to Kaliana, that is closer to the belt than Kalianpur. This would have been the reason for the discrepancy that caused the error. But when he attempted to calculate the error by evaluating the mass of Himalaya and Tibet, he made a bewildering discovery: the calculated error was three times larger than the measured one! The plumb line was deviated from the vertical by a lower angle than expected! (The attraction of the Himalaya Mountains upon the plumbline in India, Pratt 1855).
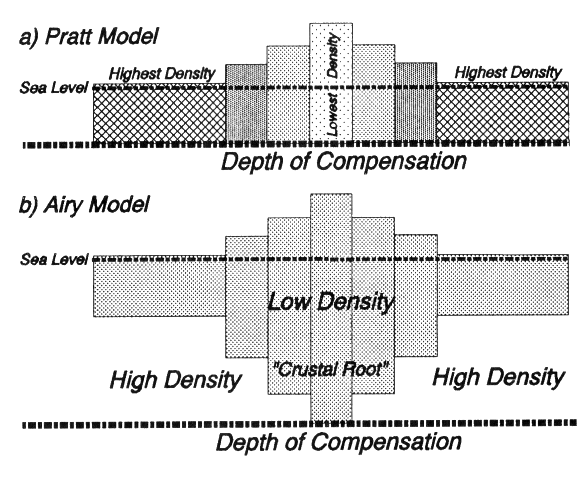
In other words, the calculation overestimated both Himalaya’s and Tibet’s mass; the mountains exerted a lower gravitational pull than the one calculated by taking into account their estimated density. Furthermore, Pratt based its calculations on the maps of the time that put the belts at less than half the height we know today; therefore he could have calculated an even greater missing mass! Pratt speculated that under the mountains there was some less dense material than the surroundings, something that would have kept the belt afloat according to Archimede’s principle. In Pratt’s hypothesis, the lower density portions of the crust are pushed higher: the thicker the crust, the lower the density, the higher the elevation.
George Biddell Airy (1801 – 1892), was a royal astronomer and mathematician. He had already carried out various researches around the Earth Sciences. He studied at Cambridge’s Trinity Collage where he became professor of mathematics and astronomy. He was also director of the Cambridge Observatory. He calculated the mean density of the Earth measuring the different attraction on a plumb line between the surface and in a deep mine. He had also calculated the polar and equatorial radii of the Earth and his geoid is still used in some reference datum in geodesy.
Airy read Pratt’s work in his London office. He thought that probably the Earth’s surface is not rigid enough to bear the load of mountain belts with no deformation. Deformation would cause a lack of mass due to the less dense material that would “fill” the bend. He opposed Pratt’s lateral density changes with a crust lighter than the subsurface on which it “floats”, with constant density but variable thickness.
Pratt’s hypothesis involved a crust with lateral variations of density, denser portion would float lower than less dense portions; Airy’s hypothesis envisaged a crust with almost constant density but varying thickness, thicker portion would float higher than thinner portions. As we know today, Pratt’s model better explains ocean floors while Airy’s is more suitable to orogenic settings.
They both contributed to the Isostasy Principle which is the application of the buoyancy principle to the Earth: an object immersed in a fluid is buoyed with a force equal to the weight of the displaced fluid. Therefore under the Earth’s crust there should be something “fluid” upon which mountains “float” like icebergs in the sea. But the movements are much slower.
The isostatic equilibrium is the reason why mountain belts rise high: they are thicker sections of the crust therefore they float at higher elevations; ocean floors have higher density so they are at lower elevations. Also, as mountain elevations are slowly reduced by erosion, their isostatic uplift compensates for the reduced thickness.
What is this fluid-but-denser material under the Earth’s crust? Why is it fluid and why mountains are formed to begin with? Later, in the early 20th century scientists would have a new weapon to investigate the deep Earth: seismology. Analyzing the behavior of seismic waves as they travel across the Earth will give researchers a way to see inside it like physicians do with human bodies using TC scans. We will see how in the next episode of Geologica.