The Shape of the Earth
I can't believe there's people today who actually think the Earth is flat. But I'll tell you one thing: it's not a sphere; it's more like ...a pear...
There was a time when scientists tried to communicate their discoveries to the world mentioning the life cycle of stars, the structure of the atom, the evolution of the universe, how the DNA codes the information of life and so on. Today scientist must point out things like “hey, the Earth his not flat!”
Scientists today are probably valuing the opinions of people who once would have had no chance to publish them. Social media allow anyone to express any idea, and their structure means that these ideas are quickly spread en masse such that they seem real to those who read about them. So the modern tendency is to say "on social networks people say that...", which would be equivalent to giving importance to the bar chatter of the past, striving to give an answer to whatever nonsense came out.
And it's probably also true that the number of people who care about spreading drivel is far greater (and more motivated) than the people who actually have knowledge.
This is why, as a geologist, I never enter into discussions regarding a flat Earth, I don't consider it something worthy of discussion at all. There is absolutely no point in discussing something obvious. It is not a matter of respecting other people’s opinions. This is not an opinion, it is a fact some people refuse to accept. There is nothing I can do about it. It would feel like discussing the existence of apples. Everybody knows apples exist. No one has created apples in order to trick us to believe in something.
What really astounds me is the fact that ancient Greeks knew the Earth must have been somehow round, since when they saw a ship from a distance, at the horizon, they first saw the sails tips, then as the distance decreased they were gradually able to see the rest. Simple as that! 3000 years ago! The Greek scholar Eratosthenes of Cyrene (276-194 BC) went to the extent of calculating the Earth’s circumference and the tilt of its axis! He was also the first to devise a global projection of the world based on a network of parallels and meridians! And we should discuss with people who believe the Earth is flat in the 21st century? No way…
But we surely can discuss the shape of the Earth. I mean I will write on what science knows today about the shape of our planet. I’m not trying to convince you. I’ll just share what I studied as a geology student and what I know as a geologist. If you don’t believe it you have a right to. I just don’t see why you should choose not to believe something I can share as a geologist (well, the Earth is my thing) while you prefer to believe someone who as no credentials at all on the subject.
There are now many people who have seen the Earth from outside and can testify it appears as a sphere. The same goes for the Moon and the Sun. Other planets and stars we can observe are apparently spherical. From a gravitational point of view, the most stable shape is that of a sphere. The gravitational field around any mass (it coincides with saying any physical object) has a spherical symmetry: it has a spherical distribution around the object. Therefore, in outer space, any fluid mass tends to acquire the shape of a sphere.
But as Newton himself stated in the 17th century, a rotating self-gravitating fluid body in equilibrium takes the form of a flattened ("oblate") ellipsoid of revolution, generated by an ellipse rotated around its minor diameter; a shape which he termed an oblate spheroid also called an oblate “ellipsoid” of revolution.
Planets and stars are rotating objects. The centrifugal force tends to swell them in the middle. So they tend to take the shape of an ellipsoid, like a sphere slightly, ahem, flattened at the poles and swollen at the equator.

The Earth is a rocky planet. But the rock it is made of is not all solid. Some of it is molten or partially so. Furthermore, for slow movements, also solid rock can behave like it is molten, meaning it can change shape. Therefore, the Earth takes the shape of an ellipsoid just because it is rotating around its axis. The ellipsoid of revolution is calculated by a sophisticated mathematical formula. It is used to project positioning data in any place of the planet. Think about Google Maps, the GPS system, etc.: they all plot any location on the Earth based on the WGS International Ellipsoid. There are several ellipsoids that have been calculated and proposed by excellent geographers and geodesists in the past. The WGS-84 ellipsoid is based on GPS satellites calculation and was proposed in 1984 by the World Geodetical System. For example, the Hayford ellipsoid introduced in 1910 is named after the US geodesist John Fillmore Hayford or the Clarke 1886 ellipsoid from the famous British geodesist Alexander Ross Clarke.
All show how the Earth, being shaped as an ellipsoid, has two different radii, the polar one being slighter shorter than the equatorial one.
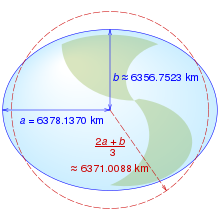
These ellipsoids are really good for practical application and are the foundation of every reference system used on the Earth to calculate geographical coordinates (latitude and longitude).
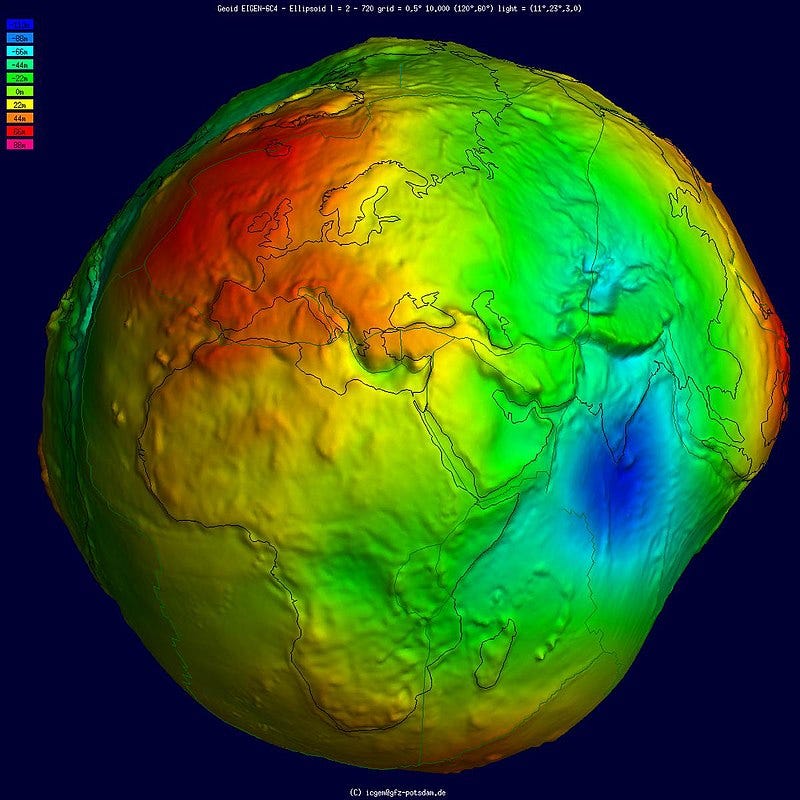
But the “actual” shape of the Earth is not as mathematically precise as a geometrical solid. Masses are unevenly distributed across the whole planet. They also change position because of plate tectonics: continents wander and oceans spread, causing a commotion during geological time. The shape of the Earth adapts to those great and slow mass displacements. The result is a shape we call “geoid”. The geoid has been defined first by Gauss as the level at which the surface of the oceans would be under the influence of only gravity and rotation of Earth. The geoid’s shape deviates slightly from the ellipsoid (it’s called undulation). If you exaggerate the deviation the geoid appears rather like a …pear!
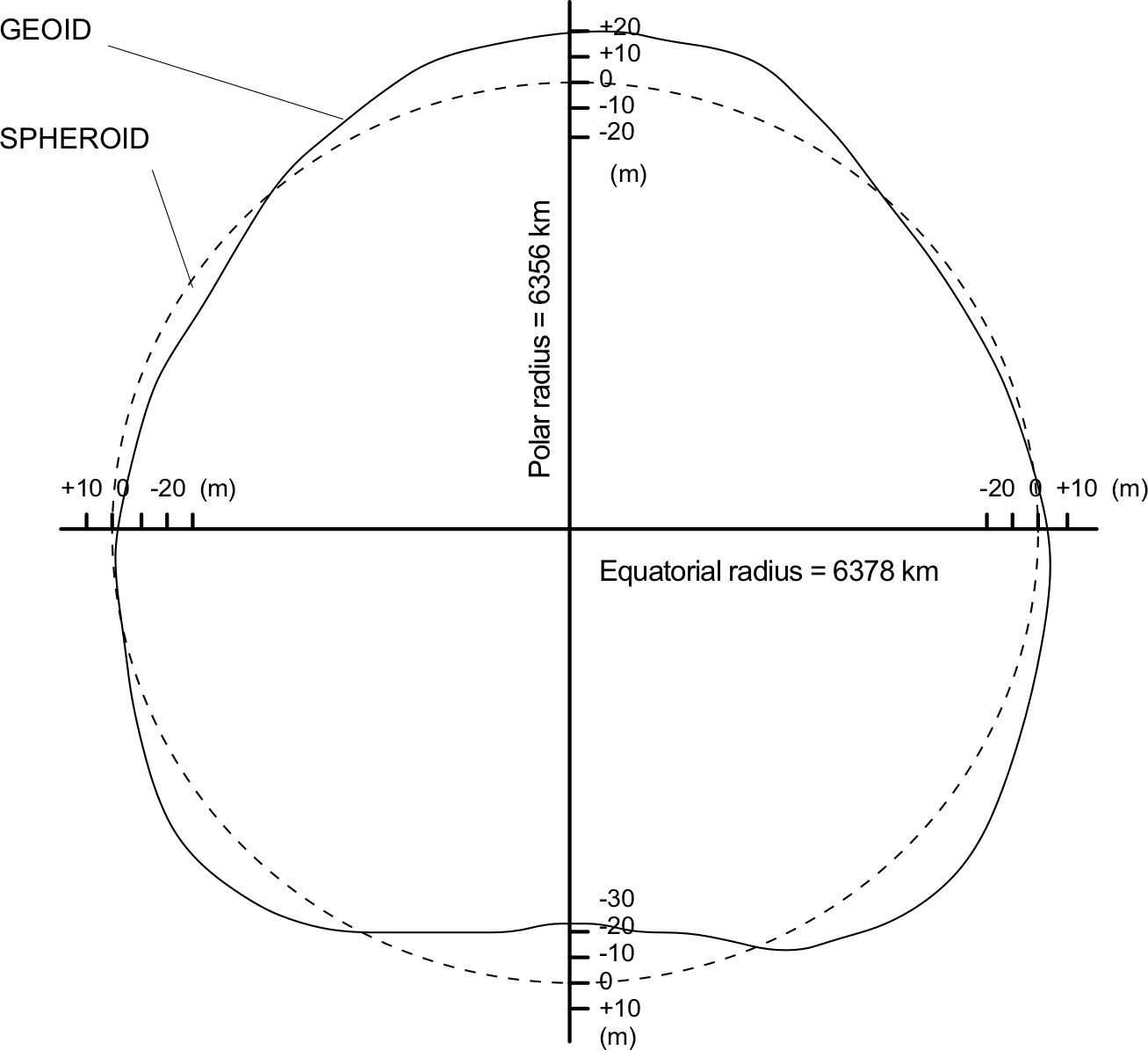
The irregular shape is due to the uneven distribution of masses within the Earth (as well as at the surface). The geoid can be calculated only through precise gravitational computations that became possible in the 20th century after satellites for geodesy became available. The surface is calculated as the result of gravitational energy and centrifugal energy of each point. Where there is mass in excess, the geoid’s surface is higher than the ellipsoids, and vice versa.
A more recent image of the geoid looks like this:
Therefore, is the Earth spherical or is it flat? Although the latter statement is not acceptable, the former is not precise. It is actually closer to a “flattened” sphere: for everyday use (for example when we plot a course on Google Maps or Waze) we use an ellipsoid (a flattened sphere, or spheroid) on which the longitude and latitude values are calculated. The ellipsoid’s deviation from a sphere are so small that the Earth from space really looks like a sphere. But it is not. The “actual” shape of a revolving and evolving planet is another matter…